こんにちは!AIサービス開発室の鈴木生雄です。早いもので気づいたらもう師走という感じですね。当社で作成しているアプリは3月末公開を目指していますので、すでに開発の佳境に入っています。それ以外にもいろいろとやりたいことがあるので、年度が切り替わっても(※当社の事業年度は11月~10月)一息つく間もありません。まあそれなりに忙しい方が悩む暇もなくていいですけどね。
ところで、去る11月6日にはOpenAI DevDayが開催され、GPT4-Turbo等の新モデルやGPTsというカスタマイズ機能が発表されました。ちなみにこの発表があってから、ChatGPT Plus(有料版)の利用者が急増したらしく、新規登録が一時停止されているとのことです。幸いにも私はすでにPlusユーザーなので、年末年始にかけていろいろと触ってみたいと思います。
それからこのGPTsを使ったイベント【CDLE名古屋主催】ChatGPTモンスターバトル!!に対戦者として参加してきました。私は残念ながら一回戦で敗退してしまったのですが、大人が数十名集まってバトルの様子を固唾を呑んで見守るという面白い時間を過ごすことができましたし、その後の懇親会では社外の人とAIを含むいろんなトピックについて話せたので、とても楽しかったです。詳しいもようについては、以下のリンク先で運営の方がブログを書いてくれていますのでぜひそちらもご覧ください。
ちなみに私がバトルで使ったモンスター(というかロボット)は以下です。見た目からは強いと思ったんですけどね~。

さて、そろそろ本題に移りたいと思います。今日は「顔の登場回数と面積から目立ち度を計算するロジック」についてお届けします。当社では顔認証の機能を搭載したアプリを開発していますので、顔認証のAIと統計学を絡めたエントリーを書いてみようということで、このテーマにしてみました。ぜひ最後までお読みいただければ幸いです。
目立ち度の定義
お示ししたテーマだけでは何のことだかわからないと思いますので、目立ち度とはいったい何なのかについて定義します。
まず前提として、複数の人物が収録されているフォトアルバムを想像してください。このフォトアルバムの中で、特定の人物が他の人物と比較して相対的にどれだけ目立っているかを数値で表現したものを目立ち度と言うことにします。
目立ち度の計算に用いるデータ
目立つという概念は個人の主観によるものなので、客観的データによって計算できる指標になるように、目立ち度を具体的に定義します。今回は、AIの顔認証タスクで求められるデータということを加味して、顔の登場回数と掲載面積を用いることにします。1冊のフォトアルバムの中に、何度も登場する顔や大きく写っている顔は目立つと言えると思うので、それなりに納得感のある数値が計算できるのではないかと思います。
以下は目立ち度の計算に用いるデータの具体例です。これ以降ではこの例を用いて具体的な計算手続きについて説明します。
| 人物 | 登場回数 (回) | 掲載面積 (cm²) |
|---|---|---|
| A | 10 | 25 |
| B | 15 | 55 |
| C | 8 | 20 |
| D | 20 | 50 |
| E | 5 | 30 |
| F | 12 | 30 |
| G | 7 | 17 |
| H | 14 | 35 |
| I | 9 | 10 |
| J | 11 | 25 |
目立ち度の計算手続き
目立ち度は、登場回数と掲載面積という二つの項目を総合評価する相対的な指標にするという方針の下、正規化、統合、Zスコアの算出という手続きで求めることを考えました。ここではそれぞれの工程においてどんなことをしているかを説明します。
正規化
はじめに、正規化について説明します。登場回数と掲載面積は単位が異なるため、評価を比較したり、統合したりできません。正規化は異なる単位の数値表現を同じ尺度に変換する手続きです。これを行うことにより、登場回数と掲載面積を比較したり統合したりできるようになります。具体的には以下のようにして、数値を0~1の尺度に収まるように変換します。
(元の値 - 母集団の中での最小値) ÷ (母集団の中での最大値 - 母集団の中での最小値) = 正規化後の値例えば、これにAさんの登場回数を当てはめてみると、(10 – 5) / (20-5) = 0.33333333…となります。この方法は”min-max normalization“と呼ばれる正規化の手法ですが、他に”“z-score normalization”と呼ばれる方法もあります。この辺りは 標準化と正規化 の説明がわかりやすいと思いましたので、そちらをご参照ください。ちなみに、“z-score normalization”はこの後のZスコアの算出の手続きで用います。
統合
正規化によって、登場回数と掲載面積の単位が揃えられました。これ以降は正規化後の値をそれぞれ登場回数のスコア、掲載面積のスコアと呼びます。次はこれらを統合したスコアを算出することで、総合評価できるようにします。統合を最も単純に行うのであれば、単純に足し合わせればよいのですが、よく考えてみると登場回数と掲載面積は、登場回数が増えると掲載面積も増えるというように、独立事象ではなく相関がありそうです。相関がある二つの指標を単純に足し合わせてしまうと、特徴量が重複して評価されてしまうことになるため、好ましくありません。そのため、登場回数と掲載面積の相関の度合いを計算して、その度合いに応じて、登場回数のスコアと掲載面積のスコアの配分(=重みづけ)を変えることにします。
最初に、登場回数と掲載面積の相関の度合い(=相関係数)を計算します。統計学には相関係数という2つのデータの間にある線形な関係の強弱を測る指標という概念およびその計算方法が確立されています。今回は”ピアソンの積率相関係数”という計算方法を用いて相関係数を求めることにしました。なお、ピアソンの積率相関係数については、相関係数(Correlation Coefficient)/ピアソンの積率相関係数(PCC)とは? がわかりやすいと思いましたので、そちらをご参照ください。また、ExcelではPEASON関数を用いて簡単に求めることができます。
それから、求めた相関係数を使って、登場回数のスコアと掲載面積のスコアの以下のように重みづけをした上で足し合わせます。そして、この結果得られたスコアを加重スコアと呼ぶことにします。
登場回数のスコア × 相関係数 + 掲載面積のスコア × (1 - 相関係数) = 加重スコアこれによって、顔の登場回数と掲載面積の総合評価のためのスコアリングができたことになります。
Zスコアの算出
正規化と統合によって総合評価の指標である0~1の尺度の値をとる加重スコアを求めることができました。しかし、このままでは母集団の中での相対的な位置をわかりやすく把握することができません。そのため、正規化の手続きのところで名前だけ触れた“z-score normalization”の手法を用いて、Zスコアと呼ばれる値を計算します。Zスコアは以下の計算で求められます。
(元の値 ‐ 平均) ÷ 標準偏差 = ZスコアZスコアは平均からどれだけ離れているかを表す指標です。また、Zスコアに変換したデータ群は平均0、標準偏差1となります。Zスコアを求めると何がうれしいかというと、平均0、標準偏差1の正規分布、すなわち標準正規分布に当てはめて累積確率を求められる点です。累積確率とは下位何%の範囲に対象のデータが入っているかを示す指標です。この点については、標準正規分布表(上側確率)の見方とエクセルでの作成 が参考になると思います。
例えば、以下ではAさんの加重スコアは0.333333333で、この時のZスコアは-0.30011191となり、ここから累積確率0.382045896が求まります。これはAさんの目立ち度が下位から約39%以内に収まっていることを表しています。このようにZスコアから累積確率を求めることによって、全体での位置をわかりやすく表現することができるようになるのです。そのため、今回においては累積確率のことを、目立ち度と呼びたいと思います。
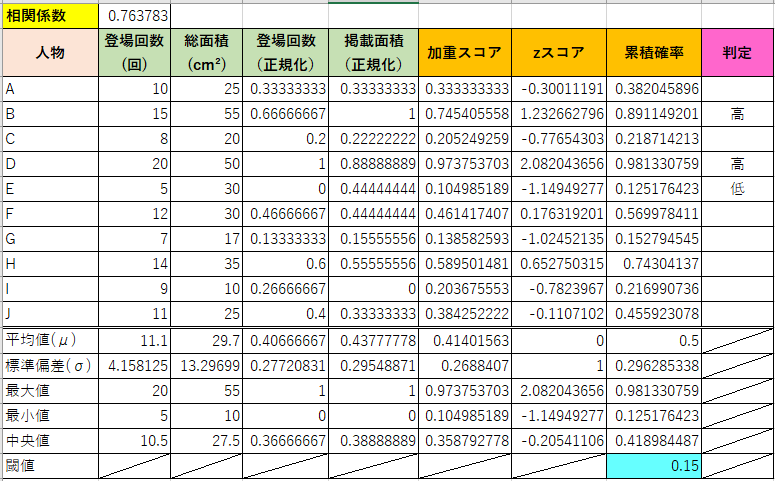
ちなみに、上の表の一番右の列では、目立ち度が上位15%以内だと「高」下位15%以内だと「低」と表示するようにしています。こうすることによって、より目立っている人と目立っていない人が明らかになりましたよね。一応、ここまでの説明の補助資料として上の表のExcelを以下からダウンロードできるようにしておきますので、興味ある方はご参照ください。
まとめ
今回はフォトアルバムにおける顔の登場回数と掲載面積という異なる単位のデータから目立ち度という総合評価の指標を計算するロジックをテーマにして、その過程で使った統計学の基本的な技法についてまとめてみました。正規化や標準化を用いて複数のデータから新たな指標を計算で求められることや、データ間で相関がある場合には相関係数によって重みづけをすることで同じ特徴量を重複して評価することを防げることが伝えられていれば幸いです。
最後に所感になりますが、統計学は今回のような初歩的な内容ですらなかなかイメージが付きづらくて個人的にとても難しいです。しかし、統計学はAIに関わる者としては避けては通れないものだとは認識しているので、今後も今回のような機会を作って知識を身に着けていきたいと思いました。
